Statically checking MPI programs against protocols

In order to check a program against a protocol, we need a program, a protocol, and a program verifier.

• Programs are written in the C programming language and make use of the MPI library interface;
• Protocols are written in a language described in this tutorial.
• Programs are verified against a protocol using VCC.

We provide an ova package containing a virtual machine with all the required software installed. Please refer to Overview of the ParTypes Artifact.

A quick tour

We start with a simple example: calculating pi via numerical integration. Pi is the area under the graph of a certain function in the interval [0..1]. The program works as follows:

• Divide the interval [0..1] in a number of subintervals
• Let processes know the number of subintervals
• Each process calculates a partial sum
• Add all the partial sums together to get Pi

Process rank 0 decides on the number of intervals and broadcasts this value among all processes. Each process calculates its local sum. In the end, a reduce operation sums all the partial sums and delivers the result at process rank 0. This process may then print the result. The protocol looks as follows.

protocol Pi {
  broadcast 0 integer
  reduce 0 sum float
}

Protocols are introduced with the keyword protocol followed by the protocol name. In this case there are two operations in sequence: broadcast 0 integer says that process rank 0 broadcasts an integer; reduce 0 sum float collects a floating point number from each process, sums them up, and delivers the result to process rank 0.

For the actual code, we consider an MPI program for calculating pi, adapted from William Gropp, Ewing Lusk, and Anthony Skjellum, Using MPI (2nd Ed.): Portable Parallel Programming with the Message-Passing Interface, MIT Press, 1999.

So now we have a protocol and a C program; there remains to check the conformance of the C code against the protocol. We need:

• The C code, pi.c

• The protocol in VCC syntax. Start by loading the above protocol in editor and press the Run button (lower right corner). This translates the protocol in VCC syntax. Write the output to a C header file, for example pi_protocol.h. The protocol header may also be generated using the ParTypes Eclipse plugin.

• The type theory in VCC format. For this we need the the ParTypes VCC library. The mpi.h header that is part of the library groups all the necessary VCC logic.

VCC limitations force us to adapt the C source code. In particular, VCC does not support:

• floating point arithmetic, and
• functions with variable number of arguments (e.g., printf).

Thus, we must filter out in pi.c the lines that contain printf, scanf, and also all those that contain floating point operations (assignments to variables h, sum, x, and mympi). Using the #ifndef _PARTYPES ... #endif macros to do the filtering, allows the code to be compiled as a normal program. In this process, we should preserve the control structure of the program, plus every MPI call and variable declaration. The resulting program must still compile and exchange the messages the original program was intended to.

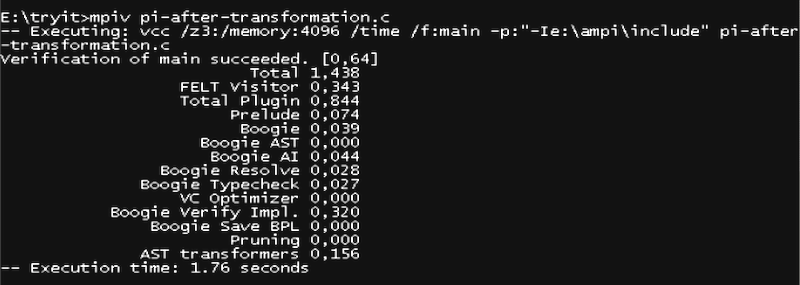
Finally, we need include the the protocol in VCC format. The final result should look similar to this. We can now run VCC after these transformations, e.g., through the mpiv.bat script that is bundled with ParTypes VCC library. VCC reports no errors, indicating that the program complies with the protocol, as shown in the screenshot below.

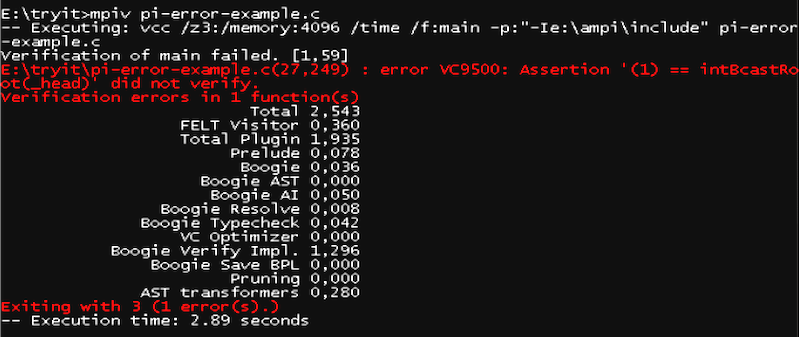
What if the program does not comply with the intended protocol? The VCC execution will then report the failed assertion(s) for protocol compliance. Consider the simple mistake of using rank 1 rather than 0 as root process the broadcast operation in the pi program, as shown here for the broadcast (MPI_Bcast) operation at line 27. The VCC output in the screenshot below indicates that 1 is not the expected root process for the broadcast operation.

Rather than installing VCC one may use the VCC page at Rise4Fun. Rise4Fun does not support loading multiple files or headers. Instead, concatenate partypes.h, the protocol in VCC format, and the code after transformation into a single file. Paste the contents of the file into Rise4Fun and run.

Carrying on

The finite differences algorithm illustrates the typical features present in a parallel application. Given an initial vector X₀, the algorithm calculates successive approximations to the solution X₁, X₂, ..., until a pre-defined maximum number of iterations has been reached. A distinguished process (usually process rank 0) disseminates the number of iterations via a broadcast operation. The same process then divides the input array among all processes. Each participant is responsible for computing its local part of the solution. Towards this end, in each iteration, each process exchanges boundary values with its left and right neighbours. When the pre-defined number of iterations is reached, process rank 0 obtains the global error via a reduce operation and collects the partial arrays in order to build a solution to the problem.

In the beginning, process rank 0 broadcasts the problem size. We write this as

broadcast 0 natural

That process rank 0 divides X₀ among all processes is rendered in ParTypes as a scatter operation.

scatter 0 float[]

Now, each process loops for a given number of iterations, nIterations. We write this as follows.

foreach i: 1..nIterations

nIterations is a variable that must be somehow introduced in the protocol. The variable denotes a value that must be known to all processes. Typically, there are two ways for processes to get to know this value:

• The value is exchanged resorting to a collective communications operation, in such a way that all processes get to know it, or
• The value is known to all processes before computation starts, for example because it is hardwired in the source code or is read from the command line.

For the former case we could for instance add another broadcast operation in the first lines of the protocol. For the latter, the protocol language relies on the val constructor, allowing one to introduce a program value in the type:

val nIterations: positive

Either solution would solve the problem. If a broadcast is used then processes must engage in a broadcast operation; if val is chosen then no value exchange is needed, but the programmer must identify the value in the source code that will inhabit nIterations.

We may now continue analyzing the loop body. In each iteration, each process sends a message to its left neighbor and another message to its right neighbor. Such an operation is again described as a foreach construct that iterates over all processes. The first process is 0; the last is size-1, where size is a distinguished variable that represents the number of processes. The inner loop is then written as follows.

foreach i: 0..size-1

When i is the rank of a process, an expression of the form i=size-1 ? 0 : i+1 denotes its right neighbor. Similarly, the left neighbor is i=0 ? size-1 : i-1.

To send a message containing a value of a datatype D, from process rank r1 to rank r2 we write message r1 r2 D. In this way, to send a message containing a floating point number to the left process, followed by a message to the right process, we write.

message i (i=0 ? size-1 : i-1) float
message i (i=size-1 ? 0 : i+1) float

So, now we can assemble the loops.

foreach i: 1..nIterations
    foreach i: 0..size-1 {
        message i (i=0 ? size-1 : i-1) float
        message i (i=size-1 ? 0 : i+1) float
    }

Once the loop is completed, process rank 0 obtains the global error. Towards this end, each process proposes a floating point number representing the local error. Rank 0 then reads the maximum of all these values. We write all this as follows.

reduce 0 max float

Finally, process rank 0 collects the partial arrays and builds a solution X_n to the problem. This calls for a gather operation.

gather 0 float[]

Before we put all the operations together in a protocol, we need to discuss the nature of the arrays distributed and collected in the scatter and gather operations. Scatter distributes X₀, dividing it in small pieces; gather collects the subarrays to build X_n. The arrays in scatter/gatherk protocols always refer to the whole array, not to the subarrays. So, we instead write:

scatter 0 float[n]
...
gather 0 float[n]

Variable n must be introduced somehow (by means of a val, broadcast, or allreduce). In this case n is exactly the problem size that was broadcast before. So we name the value that rank 0 provides as follows.

broadcast 0 n:natural

But n cannot be an arbitrary non-negative number. It must evenly divide X₀. In this way, each process gets a part of X₀ of equal length, namely length(X0) / size, and we do not risk accessing out-of-bound positions when manipulating the subarrays. So we would like to make sure that the length of X₀ is such that length(X0) % size = 0.

For this we use a refinement datatype. Rather that saying that n is a natural number we say that it is of datatype {x: natural | x % size = 0}.

As an aside, datatype natural can be expressed as {x: integer | x >= 0}. Similarly, datatype positive abbreviates {x: integer |x > 0}.

Finally, syntax float[n] is the abbreviation of a refinement type {x: float[] | length(x) = n}.

Putting everything together, the protocol for the finite differences algorithm is as follows.

protocol FiniteDifferences {
    val n: {x: natural | x % size = 0}
    broadcast 0 nIterations: integer
    scatter 0 float[n]
    foreach i: 1 .. nIterations
        foreach i: 0 .. size-1 {
            message i (i=0 ? size-1 : i-1) float
            message i (i=size-1 ? 0 :i+1) float
        }
    reduce 0 max float
    gather 0 float[n/size]
}

Protocols also allow for a restriction on the required number of processes. For example, the finite differences protocol could have been written as follows,

protocol FiniteDifferences (size >= 2) {...}

indicating that at least two processes are necessary for the protocol to be correct. If absent, ParTypes adds the necessary restriction automatically: size >= 2 if the protocol contains a message, and size >= 1 otherwise. If there is a message in the protocol then at least two processes are required, since a process sending a message to itself will result in a deadlock.

Try adding (size >= 1) to the protocol example above, and see what happens when you press run.

The topology underlying the protocol for the finite differences is that of a ring: a linear array with a wraparound link. If a different mapping of ranks to processes is to be used, a new protocol must be derived.

It turns out that the language of protocols is flexible enough to encode topologies in integer arrays. Such a topology may then be made known to all processes, in such a way that processes exchange messages as per the particular topology.

This flexibility is particularly useful for applications that dynamically adequate the protocol to, say, the load of messages exchanged.

A datatype of the form

{t: {x: integer | 0 <= x and x < size}[size] |
    forall y: (y in 0..length(t)-1) => t[y] != y}

encodes a one-dimensional network topology, where t[x]=y means x is a direct neighbor of y: each node has one direct neighbor (a number between 0 and size-1) that is different from itself.

Such a type, call it D, can be distributed among all processes by, say, rank 0.

broadcast 0 topology:D

Thereafter each process can exchange a message with its neighbor, as in:

foreach i: 0 .. length(topology)-1
    message i topology[i] float

For example, a right-to-left ring topology of length five can be encoded as [4,0,1,2,3]. A complete protocol for this topology is as follows.

protocol TopologyPassing1D {
    broadcast 0 topology: {b: {x: integer | 0 <= x and x < size}[size]
        | forall y: (y in 0 .. length(b)-1) => (b[y] != y)}
    foreach i: 0 .. length(topology)-1
        message i topology[i] float
}

The encoding above requires all processes to have a direct neighbour. How can one encode a topology when this is not the case? Think of a star or a line.

One possibility is to weaken the above condition on the elements of the array, while strengthening the subsequent message passing loop. We could for example drop the restriction that t[y]!=y and encode a right-to-left line of length five as [0,0,1,2,3], a 0-centered star as [0,0,0,0,0], and a full binary 0-rooted tree of depth 3 as [0,0,0,1,1,2,2]. In all cases, rank 0 has no direct neighbor. And this causes a problem if we try to send a message from i to topology[i], as in the above example.

Given that the topology is a data structure known to all processes we can make use of a primitive called collective choice. We start by broadcasting the topology and enter the loop as before. Then, within the loop, a message is exchanged only if the topology array contains a valid entry.

protocol TopologyChoice {
    broadcast 0 topology: {x: integer[] | 0 <= length(x) and length(x) <= size}
    foreach i: 0 .. length(topology)-1 {
        if (0 <= topology[i] and topology[i] < size and i != topology[i])
            message i topology[i] float
        else
            {}
    }
}

Arbitrary topologies can be encoded, e.g., using an adjacency matrix. For example a partially connected mesh topology:

could be encoded with two arrays, one for the sources ([0,0,1,2,3,4]), and another for the targets ([1,4,3,4,4,5]). A protocol where rank 0 broadcasts the two arrays and then each process exchanges one message with its neighbour can be written as follows.

protocol ArbitraryTopology {
    broadcast 0 source: 
        {s: integer[] |
          forall i: (i in 0 .. length(s)-1) =>
            (0 <= s[i] and s[i] < size)}
    broadcast 0 target: 
        {t: integer[] |
            (forall i: (i in 0 .. length(t)-1) =>
                (0 <= t[i] and t[i] < size and t[j] != source[y])) and
            length(t) = length(source)}
    foreach i: 0 .. length(source)-1
        message source[i] target[i] float
}

Describing the number of processes

The special variable size denotes the number of processes. Its type is inferred from the protocol as follows:

• If the protocol does not contain point-to-point communications (message), then size is of type positive;
• Otherwise size is of type {x:integer|x>1}.

What if we want to say that the number of the number of processes is even? One can add a proposition in the signature of the protocol to describe the type of size. For example, in the following protocol,

protocol EvenNumberOfProcesses size % 2 = 0 and size >= 2 {
  message 1 0 integer
}

variable size is of type {x: integer | size % 2 = 0 and size >= 2}. If the protocol does not contain messages, then we may write:

protocol EvenNumberOfProcesses size % 2 = 0 and size >= 7 {
  broadcast 6 integer
}

The syntax of datatypes

Datatypes in ParTypes are of the form integer, float, D[], D[i], {x:D|p}, natural and positive where D is any datatype, i is a term, x is a variable name, and p is a proposition.

The first two, integer and float, are primitive types, equivalent to int and float in the C programming language.

D[i] is an array type, an ordered collection of values of type D that can be indexed, with i being an expression denoting the length or size of the collection. The i parameter is optional. A datatype of the form D[i] abbreviates {a: D[] | length(a)=i}. Due to limitations of the implementation, types of the form D[][] are not accepted. One cannot have an array of arrays.

{x:D|p} denotes a refinement type. D can by any other type including other refinement types. Refinement types restrict the values allowed for this datatype. For example, {x:integer | x >= 0} denotes the set of natural numbers.

natural and positive are derived types, simple abbreviations for refinement types {x:integer | x >= 0} and {x:integer | x > 0} respectively.

ParTypes supports a large number of operators for propositions and terms. Floating point expressions are not supported.

Propositions include equality operators (i = i, i != i), comparison operators (i < i, i <= i, i > i, i >= i), conditional expressions (p ? i : i), universal quantification (forall x: p), implication (p => p), conjunction (p and p), disjunction (p or p) and negation (not p). For convenience there is also the x in i1 .. i2 operator, which is equivalent to writing i1 <= x and x <= i2.

Terms include arithmetic operators (i + i, i - i, i * i, i / i, i % i), integer literals (ex. 0, 255, 0xFF), boolean literals (true or false), variable reference (ex. x, data), array reference (ex. x[0]), array literal (ex. #[0,3,4,5,2]) and the length operator (length(x)).

The length operator can be used to restrict the size of arrays in refinements. For example: {x:integer[] | length(x) % 2 = 0}

Examples

• fdiff.prot
• laplace.prot
• pi.prot
• parallelJacobi.prot
• matrixmul.prot
• parallelDot.prot
• topologyPassing1D.prot
• topologyChoice.prot
• arbitraryTopology.prot
• nbodypipe.prot
• diffusion1D.prot